CUDA 实践:Winograd 卷积 | CUDA
对于小尺寸的卷积核,Winograd 卷积也是一种常用的优化方法。其基本原理是基于最小滤波算法用加法来替代乘法,以此来降低卷积运损啊的乘法复杂度。
算法原理
一维 Winograd 卷积
对于输入 $[d_0, d_1, d_2, d_3]$,卷积核 $[g_0, g_1, g_2]$,步长为 1 的卷积运算,正常的运算过程如下:
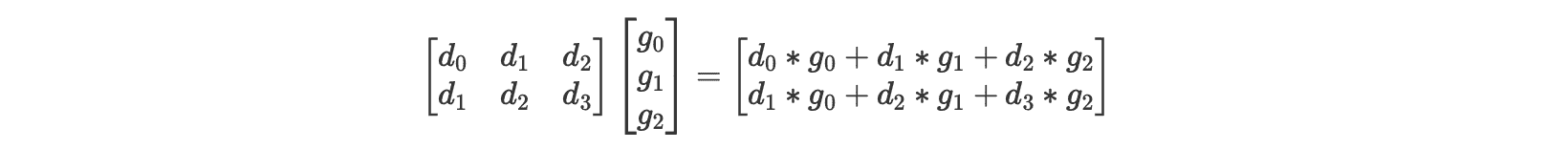
总共包含 6 次乘法和 4 次加法。
如果使用 $F(m, r) = F(2, 3)$(m 是输出的尺寸,r 是卷积核的尺寸)的 Winograd 算法进行运算:

计算中 d 是卷积核,可以在提前计算好, 因此总共只要 4 次乘法和 8 次加法。
上述操作可以写成矩阵形式:
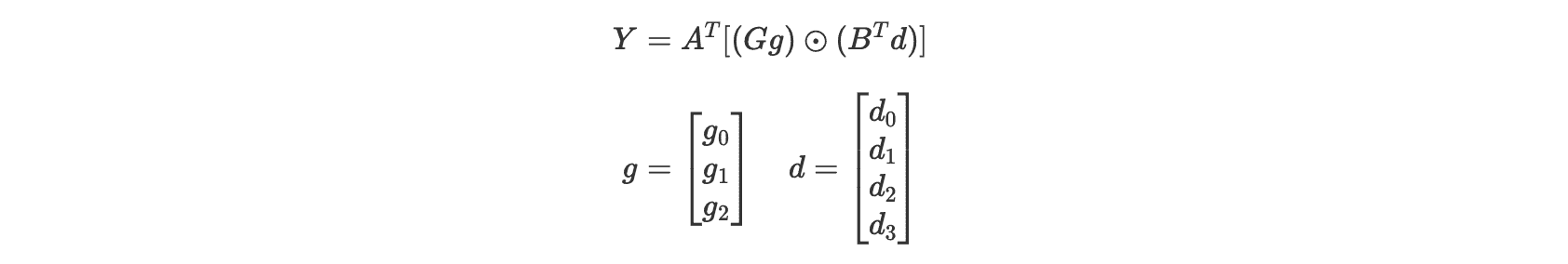
其中 $\odot$ 是逐元素相乘。对于 $F(2, 3)$,变换矩阵 $A, B, G$ 如下:
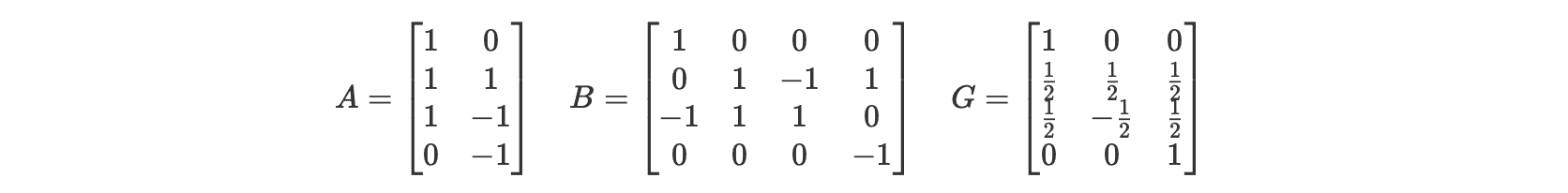
二维 Winograd 卷积
对于二维 Winograd 卷积,容易从一维形式推广得到:
$${Y~=A^T[(GgG^T)\odot(B^TdB)]A=A^T[U\odot V]A=A^TMA}$$
当 $m = 2, r = 3$ 时,$F(m * m, r * r) = F(2 * 2, 3 * 3)$ 表示输出为 2x2,卷积核为 3x3,步长为 1 的二维卷积运算,可以推断出此时输入的尺寸为 4x4。
代码实现
常量折叠
在实际实现时,如果严格按照矩阵形式公式进行实现,会发现需要的乘法和加法次数和非矩阵形式的公式并不一致,这是因为矩阵形式的公式只是用于描述计算的流程。在实际运算的时候需要提前进行常量折叠,即将矩阵中的 0 和 1 提前进行运算。 比如在计算 $B^Td$ 的时候,对于 $B^T$ 中的 0 和正负 1,直接写死成加法和减法即可,这样原本所需的 64 次乘法全都可以省掉了,加减法也从 48 次减少到 20 次(负数视作一次减法)。
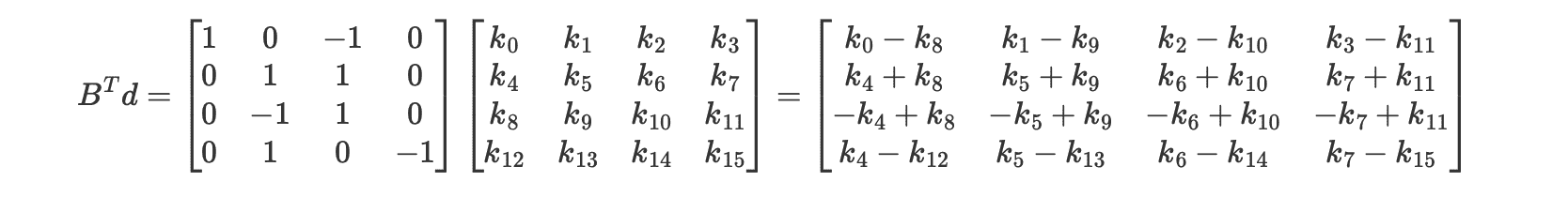
计算流程
1. 卷积核变换
根据变换矩阵提前计算得到变换后的卷积核:

2. 输入变换
在前面的描述中,$F(2 * 2, 3 * 3)$ 只能处理 4x4 的输入,对于尺寸更大的输入,首先要进行切块,然后进行数据重排以获得更好的数据局部性:
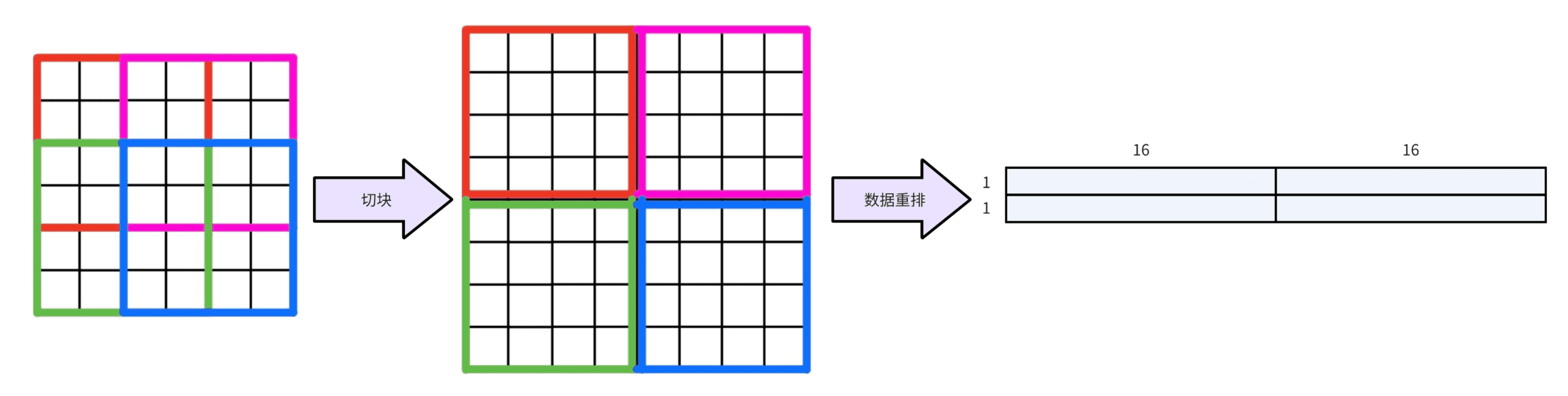
在每个 4x4 的输入块中,卷积核可以完成 4 次卷积运算。和滑窗卷积类似,每两个相邻的 4x4 块也需要有一定的重叠,重叠的大小为 $r - 1$。
3. Winograd 卷积
现在我们已经有了变换后的卷积核 $GgG^T$,也有了连续的数据块 $d$,现在只需要根据二维 Winograd 公式完成剩余的计算既可以得到 2x2 的输出数据块。
4. 输出变换
上一步得到的 2x2 的输出数据块是连续,但是每个块在整个输出 feature map 中却是不连续的(4 个元素分布在 2 行中),需要还需要一次变换:

完整代码在 zh0ngtian/cuda_learning。
TODO
- 使用共享内存,以 block 为单位考虑问题
- 优化数据排布,参考下图改善通道维度的数据局部性

参考
CUDA 实践:Winograd 卷积 | CUDA